1. 因果推断中的挑战
因果推断的目标是估计处理(Treatment)对结果(Outcome)的影响,特别是在观测数据(非随机试验)中,我们通常面临混杂偏倚(Confounding Bias)的问题。主流的因果推断方法通常有两大类:
- 倾向评分方法(PSM, Propensity Score Methods):例如逆概率加权(IPW, Inverse Probability Weighting),使用倾向评分(treatment assignment probability)来调整不同组间的可比性。
- 结果回归方法(Outcome Regression, OR):直接用回归模型估计治疗组和对照组的结果,然后计算它们的差值。
但这两种方法各有局限,例如IPW依赖于倾向评分模型的准确性,而OR依赖于结果回归模型的正确性。如果模型错误,估计结果就会有偏差。因此,需要双重稳健(Doubly Robust, DR)的方法。
2. 双网络深度因果模型(DR-DCM)的核心思想
DR-DCM结合倾向评分模型和结果回归模型,并使用深度学习(Deep Learning)来增强建模能力,具体包括:
- 倾向评分网络(Propensity Score Network, PSN):用于估计个体接受处理的概率 p(T=1∣X)。
- 结果回归网络(Outcome Regression Network, ORN):用于分别预测处理组和对照组的结果Y^(T=1,X)和Y^(T=0,X)。
- 双重稳健校正(Doubly Robust Adjustment):结合倾向评分加权(IPW)和结果回归模型,进行最终的因果效应估计。
数学表达
对于每个个体i,观测数据 (Xi,Ti,Yi):
- Xi:个体特征
- Ti:处理变量(1=接受处理,0=未接受处理)
- Yi:观察到的结果
1. 估计倾向评分(Propensity Score):
由倾向评分网络进行估计。
2. 估计结果回归(Outcome Regression):
由结果回归网络进行估计。
3. 计算双重稳健估计量(Doubly Robust Estimator):
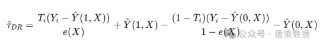
该估计量具有 双重稳健性,即即使e(X)或Y^(T,X)其中之一估计不准,因果效应τ^DR仍然是一致估计。
3. DR-DCM 的优势
- 双重稳健性:即使一个模型(PSN或ORN)错误,仍然可以得到合理的因果效应估计。
- 深度学习增强建模能力:深度神经网络能够自动学习复杂的非线性关系,提高倾向评分和结果回归的估计精度。
- 适用于高维和非线性因果关系:传统因果推断方法在高维数据或复杂因果结构下可能表现不佳,而DR-DCM通过神经网络提升了估计能力。
示例:
接下来我们生成一个示例数据集,然后使用PyTorch实现双网络深度因果模型:
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
import matplotlib.pyplot as plt
import seaborn as sns
# 1. 生成模拟数据
np.random.seed(42)
n = 5000 # 样本量
X = np.random.normal(0, 1, (n, 5)) # 5 个协变量
T = np.random.binomial(1, p=1 / (1 + np.exp(-X[:, 0] - X[:, 1])), size=n) # 倾向评分与X0, X1相关
Y0 = X[:, 2] + np.random.normal(0, 1, n) # 对照组
Y1 = X[:, 2] + X[:, 3] + np.random.normal(0, 1, n) # 处理组
Y = T * Y1 + (1 - T) * Y0 # 观测结果
dev = torch.device("cuda" if torch.cuda.is_available() else "cpu")
X_tensor = torch.tensor(X, dtype=torch.float32).to(dev)
T_tensor = torch.tensor(T, dtype=torch.float32).to(dev)
Y_tensor = torch.tensor(Y, dtype=torch.float32).to(dev)
data_loader = DataLoader(TensorDataset(X_tensor, T_tensor, Y_tensor), batch_size=64, shuffle=True)
# 2. 定义神经网络(倾向评分网络和结果回归网络)
class NeuralNet(nn.Module):
def __init__(self, input_dim):
super(NeuralNet, self).__init__()
self.model = nn.Sequential(
nn.Linear(input_dim, 16),
nn.ReLU(),
nn.Linear(16, 8),
nn.ReLU(),
nn.Linear(8, 1)
)
def forward(self, x):
return self.model(x)
# 倾向评分网络(PSN)
propensity_net = NeuralNet(input_dim=5).to(dev)
propensity_optimizer = optim.Adam(propensity_net.parameters(), lr=0.01)
criterion = nn.BCEWithLogitsLoss()
# 3. 训练倾向评分网络
for epoch in range(10):
for batch_x, batch_t, _ in data_loader:
propensity_optimizer.zero_grad()
logits = propensity_net(batch_x).squeeze()
loss = criterion(logits, batch_t)
loss.backward()
propensity_optimizer.step()
# 4. 训练结果回归网络
outcome_net = NeuralNet(input_dim=6).to(dev) # 输入包括X和处理变量T
outcome_optimizer = optim.Adam(outcome_net.parameters(), lr=0.01)
criterion = nn.MSELoss()
for epoch in range(10):
for batch_x, batch_t, batch_y in data_loader:
outcome_optimizer.zero_grad()
inputs = torch.cat([batch_x, batch_t.unsqueeze(1)], dim=1) # 处理变量T拼接到输入特征中
predictions = outcome_net(inputs).squeeze()
loss = criterion(predictions, batch_y)
loss.backward()
outcome_optimizer.step()
# 5. 计算双重稳健估计
with torch.no_grad():
e_x = torch.sigmoid(propensity_net(X_tensor)).squeeze() # 倾向评分
y1_pred = outcome_net(torch.cat([X_tensor, torch.ones(n, 1).to(dev)], dim=1)).squeeze()
y0_pred = outcome_net(torch.cat([X_tensor, torch.zeros(n, 1).to(dev)], dim=1)).squeeze()
doubly_robust = (T_tensor * (Y_tensor - y1_pred) / e_x + y1_pred) - \
((1 - T_tensor) * (Y_tensor - y0_pred) / (1 - e_x) + y0_pred)
ate_dr = doubly_robust.mean().item()
print(f"Doubly Robust ATE Estimate: {ate_dr:.4f}")
生成模拟数据:
自变量X,其中X0,X1影响倾向评分,X2,X3影响结果。 处理变量T服从一个逻辑回归概率模型。 结果变量Y由T以及X生成。
构建神经网络:
- 倾向评分网络(PSN):估计P(T=1∣X)。
- 结果回归网络(ORN):估计Y^(T=1,X)和Y^(T=0,X)。
训练倾向评分网络:
使用二元交叉熵损失(BCEWithLogitsLoss),训练用于分类。
训练结果回归网络:
目标是预测Y,使用均方误差损失(MSELoss)。 训练时,输入数据(X,T) 共同影响结果。
计算双重稳健估计量(Doubly Robust Estimator):
计算倾向评分e(X)。 预测两个处理组的结果Y^(1,X)和 Y^(0,X)。 使用双重稳健公式计算平均处理效应(ATE)。
我们可以使用Matplotlib和Seaborn绘制图形来更直观地理解数据和模型的结果:
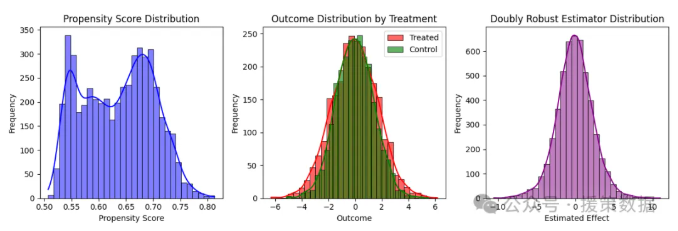
- 倾向评分分布图(Propensity Score Distribution):查看不同处理组的倾向评分分布,确保 PSN 学到了合理的分布。
- 处理组vs.对照组的结果分布(Outcome Distribution by Treatment):可视化处理组和对照组的结果Y分布情况。
- 双重稳健估计量分布(Doubly Robust Estimator Distribution):观察最终的因果效应估计值。
# 6. 数据可视化
plt.figure(figsize=(12, 4))
# 倾向评分分布
plt.subplot(1, 3, 1)
sns.histplot(e_x.cpu().numpy(), bins=30, kde=True, color='blue')
plt.title("Propensity Score Distribution")
plt.xlabel("Propensity Score")
plt.ylabel("Frequency")
# 处理组 vs 对照组的结果分布
plt.subplot(1, 3, 2)
sns.histplot(Y[T == 1], bins=30, kde=True, color='red', label="Treated", alpha=0.6)
sns.histplot(Y[T == 0], bins=30, kde=True, color='green', label="Control", alpha=0.6)
plt.title("Outcome Distribution by Treatment")
plt.xlabel("Outcome")
plt.ylabel("Frequency")
plt.legend()
# 双重稳健估计分布
plt.subplot(1, 3, 3)
sns.histplot(doubly_robust.cpu().numpy(), bins=30, kde=True, color='purple')
plt.title("Doubly Robust Estimator Distribution")
plt.xlabel("Estimated Effect")
plt.ylabel("Frequency")
plt.tight_layout()
plt.show()
— 文章来源 策源数据








Comments NOTHING