1. 倾向得分的基本概念
在因果推断中,倾向得分是一个条件概率:
其中:
- T是处理(treatment)变量(1 表示接受处理,0 表示未接受处理)。
- X是协变量(covariates),即可能影响处理选择和结果的因素。
- e(X) 表示在给定 X的情况下,个体接受处理的概率。
倾向得分的主要作用是减少混杂因素(confounding bias),使得处理组和对照组在X的条件下更加可比,从而更准确地估计处理的因果效应。
2. 传统倾向得分估计方法
传统方法通常使用逻辑回归(Logistic Regression)或者机器学习方法(如随机森林、梯度提升树)来估计e(X)。这些方法可能在低维度数据中表现良好,但在复杂、高维数据(如图像、文本、时间序列)中可能难以准确建模。
3. 深度倾向得分模型(DPSM)
深度倾向得分模型利用神经网络的强大表达能力来估计倾向得分,适用于高维、复杂的协变量X。DPSM 主要包括以下几个核心部分:
(1) 神经网络结构
DPSM 采用深度神经网络(Deep Neural Network, DNN)来学习从协变量到倾向得分的映射:
- 输入层:接受协变量X(可能包括数值、类别数据,甚至图像或文本)。
- 隐藏层:多个非线性变换(如ReLU、Sigmoid),可以捕捉复杂的特征交互。
- 输出层:使用 Sigmoid 激活函数,输出范围为 (0,1),表示估计的倾向得分。
(2) 训练过程
使用交叉熵损失函数(Binary Cross-Entropy Loss)进行优化:
采用随机梯度下降(SGD)或Adam优化器进行训练。
(3) 处理不平衡问题
在因果推断中,处理组和对照组的样本可能严重不均衡(如医疗试验中,某种药物只给少数病人服用)。DPSM 通过以下策略应对:
- 权重调整:对损失函数加权,以平衡处理组和对照组的贡献。
- 对抗学习(Adversarial Learning):引入对抗网络来增强倾向得分估计的稳健性。
4. DPSM 的优势
a 适用于高维和复杂数据(如图像、文本、时间序列)。
b 能够捕捉复杂的非线性关系,比传统方法更具表现力。
c 可以集成对抗学习,减少倾向得分估计的偏差。
但也存在挑战:
a 需要大量数据才能有效训练。
b 计算成本较高,训练时间长。
c 可能存在过拟合问题(需要正则化、Dropout 等技术)。
5. DPSM 的应用场景
- 医疗研究:评估治疗效果,控制混杂因素(如病人的年龄、病史等)。
- 经济学:分析政策干预的因果效应(如税收政策对就业率的影响)。
- 市场营销:评估广告投放策略的因果影响(如某种营销活动是否增加了销售量)。
- 社交网络:分析用户行为的因果关系(如推荐系统对用户参与度的影响)。
以下,我们尝试用 PyTorch 实现一个深度倾向得分模型(DPSM),训练神经网络来估计倾向得分!我们将使用PyTorch构建一个DPSM,并应用它来估计处理概率(倾向得分),然后使用逆概率加权(IPW, Inverse Probability Weighting)计算平均处理效应(ATE, Average Treatment Effect)。
步骤:
生成模拟数据:
生成协变量X(5 维特征)。 生成处理变量T(根据X的非线性函数)。 生成结果变量Y(受X和T影响)。
构建深度倾向得分模型:
用神经网络学习 P(T=1∣X)。
使用倾向得分进行因果推断:
计算逆概率加权估计处理效应。 可视化倾向得分分布,分析其合理性。
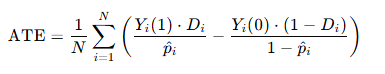
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 1. 生成模拟数据
np.random.seed(42)
n_samples = 1000
X = np.random.normal(0, 1, (n_samples, 5)) # 5 维协变量
# 生成非线性处理概率
T_prob = 1 / (1 + np.exp(- (X[:, 0] * X[:, 1] - X[:, 2] ** 2 + X[:, 3] * 0.5)))
T = (np.random.rand(n_samples) < T_prob).astype(int) # 0/1 处理变量
# 生成结果变量 Y
Y = 2 * T + X[:, 0] + 0.5 * X[:, 1] - 0.3 * X[:, 2] + np.random.normal(0, 0.5, n_samples)
# 2. 数据预处理
scaler = StandardScaler()
X = scaler.fit_transform(X)
X_train, X_test, T_train, T_test = train_test_split(X, T, test_size=0.2, random_state=42)
# 3. 定义深度倾向得分模型(DPSM)
class DPSM(nn.Module):
def __init__(self, input_dim):
super(DPSM, self).__init__()
self.model = nn.Sequential(
nn.Linear(input_dim, 16),
nn.ReLU(),
nn.Linear(16, 8),
nn.ReLU(),
nn.Linear(8, 1),
nn.Sigmoid()
)
def forward(self, x):
return self.model(x)
# 4. 训练 DPSM
model = DPSM(input_dim=5)
criterion = nn.BCELoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
def train_model(model, X_train, T_train, epochs=100):
X_tensor = torch.tensor(X_train, dtype=torch.float32)
T_tensor = torch.tensor(T_train, dtype=torch.float32).unsqueeze(1)
for epoch in range(epochs):
optimizer.zero_grad()
outputs = model(X_tensor)
loss = criterion(outputs, T_tensor)
loss.backward()
optimizer.step()
if (epoch+1) % 20 == 0:
print(f"Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}")
return model
model = train_model(model, X_train, T_train, epochs=200)
# 5. 计算倾向得分
def compute_propensity_scores(model, X):
with torch.no_grad():
X_tensor = torch.tensor(X, dtype=torch.float32)
scores = model(X_tensor).numpy().flatten()
return scores
e_scores = compute_propensity_scores(model, X_test)
# 6. 计算逆概率加权(IPW)估计 ATE
# 确保 Y 也按照相应的测试集划分
Y_train, Y_test = train_test_split(Y, test_size=0.2, random_state=42)
# 重新计算 ATE(IPW 估计)
ipw_weights = 1 / (e_scores * T_test + (1 - e_scores) * (1 - T_test))
ATE_IPW = np.mean((T_test * Y_test) / e_scores - ((1 - T_test) * Y_test) / (1 - e_scores))
print(f"ATE (IPW 估计) = {ATE_IPW:.4f}")
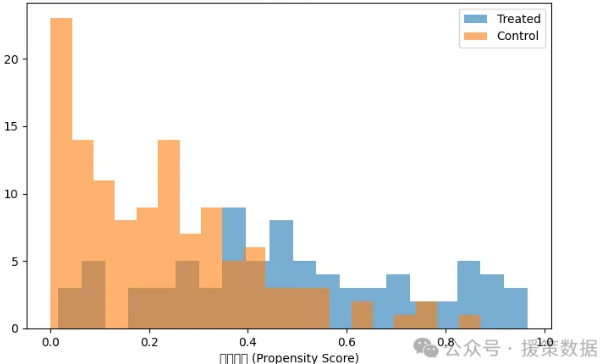
# 7. 可视化倾向得分分布
plt.figure(figsize=(8, 5))
plt.hist(e_scores[T_test == 1], bins=20, alpha=0.6, label='Treated')
plt.hist(e_scores[T_test == 0], bins=20, alpha=0.6, label='Control')
plt.xlabel("倾向得分 (Propensity Score)")
plt.ylabel("样本数")
plt.legend()
plt.title("倾向得分分布")
plt.show()
生成数据:
5 维协变量X影响处理变量T。 - Y 由T和 X线性影响。
训练 DPSM:
3 层神经网络学习 P(T=1∣X)。 使用二元交叉熵损失训练。
估计处理效应:
计算倾向得分 e(X)。 用IPW 估计 ATE。
可视化:
绘制倾向得分分布,查看处理组和对照组的倾向得分差异。








Comments NOTHING