1. 反事实推断的核心问题
因果推断的核心挑战在于反事实(Counterfactual)无法直接观察。例如,在医疗试验中,对于一个接受了治疗T=1的病人,我们只能观察到他的健康状况Y(1),但无法知道如果他未接受治疗(T=0),他的健康状况Y(0)会如何。这就形成了“缺失的反事实”问题。
目标是估计个体处理效应(Individual Treatment Effect, ITE):
但由于只能观察到其中之一,估计这一差值变得困难。
2. 生成对抗网络(GANs)的引入
生成对抗网络(GANs)由一个生成器(Generator, G)和一个判别器(Discriminator, D)组成。生成器G试图生成逼真的数据,而判别器D试图区分真实数据和生成的数据。这种对抗训练使得G逐渐学习到数据的真实分布。
在反事实推断中,GANs可用于学习数据分布,并生成潜在的反事实结果。CF-GANs的目标是利用GANs生成个体的反事实结果,从而更准确地估计因果效应。
3. CF-GANs 的架构
CF-GANs 主要包括三个部分:
生成器 G:
以个体特征X和处理T作为输入,学习生成缺失的反事实结果,即:Y^(T)=G(X,T,Z),其中Z是噪声变量。 生成器试图使合成的反事实数据与真实数据分布匹配。
判别器 D:
试图区分真实的观察结果Y(T)和生成器生成的反事实结果Y^(T)。 通过对抗训练,迫使生成器生成更逼真的反事实数据。
重构损失(Reconstruction Loss):
由于个体的真实观察结果是已知的,CF-GANs还会引入一个重构损失,确保当 GANs 生成已观察的结果时,与真实值保持一致。 公式上,若个体i观测到Y(T),那么要求:G(X,T)≈Y(T)G(X, T)
4. CF-GANs 的训练过程
CF-GANs 训练过程包括以下步骤:
- 初始化生成器和判别器的参数。
- 使用已观测数据训练判别器,使其能够分辨真实观察值和生成值。
- 训练生成器,使其生成的反事实数据与真实数据分布匹配。
- 利用观测数据计算重构损失,确保生成的结果尽可能接近真实数据。
- 迭代优化,直到生成器能够逼真地模拟反事实分布。
5. CF-GANs 在因果推断中的应用
- 医疗与精准医学:估计某种治疗对个体病人的影响,预测未接受治疗时的病情变化。
- 经济学与政策评估:模拟不同政策实施下的经济结果,例如评估最低工资政策对就业率的影响。
- 推荐系统:估计如果用户未选择某个产品,他们是否会选择另一种产品,从而优化个性化推荐。
示例
我们可以用一个模拟医疗试验的数据集来演示 CF-GANs 的原理。假设我们有一个数据集,包含患者的特征、是否接受了治疗(T),以及治疗后的健康状况(Y)。我们的目标是使用 CF-GANs 生成反事实结果,并估计个体治疗效应(ITE)。
示例数据
- 特征(X):患者的年龄、血压、体重等。
- 处理(T):是否接受治疗(0 或 1)。
- 观察结果(Y):患者的健康评分(0-100),表示健康状况。
接下来,我们用 Python 代码模拟一个小型数据集,并搭建一个简单的 CF-GANs 框架。
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
# Step 1: 生成模拟数据
def generate_data(n=1000):
np.random.seed(42)
X = np.random.randn(n, 3) # 三个特征(例如:年龄、血压、体重)
T = np.random.binomial(1, 0.5, n) # 处理(0 或 1)
Y0 = 50 + 10 * X[:, 0] + 5 * X[:, 1] + np.random.randn(n) * 5 # 未治疗的结果
Y1 = Y0 + 10 + np.random.randn(n) * 2 # 治疗后的结果
Y = T * Y1 + (1 - T) * Y0 # 观察到的结果
return X, T, Y, Y0, Y1
X, T, Y, Y0, Y1 = generate_data()
dataset = TensorDataset(torch.tensor(X, dtype=torch.float32),
torch.tensor(T, dtype=torch.float32).unsqueeze(1),
torch.tensor(Y, dtype=torch.float32).unsqueeze(1))
train_loader = DataLoader(dataset, batch_size=64, shuffle=True)
# Step 2: 定义 CF-GANs 结构
class Generator(nn.Module):
def __init__(self, input_dim):
super(Generator, self).__init__()
self.model = nn.Sequential(
nn.Linear(input_dim + 1, 16),
nn.ReLU(),
nn.Linear(16, 16),
nn.ReLU(),
nn.Linear(16, 1)
)
def forward(self, x, t):
return self.model(torch.cat([x, t], dim=1))
class Discriminator(nn.Module):
def __init__(self, input_dim):
super(Discriminator, self).__init__()
self.model = nn.Sequential(
nn.Linear(input_dim + 1, 16),
nn.ReLU(),
nn.Linear(16, 16),
nn.ReLU(),
nn.Linear(16, 1),
nn.Sigmoid()
)
def forward(self, x, y):
return self.model(torch.cat([x, y], dim=1))
# 初始化模型
generator = Generator(input_dim=3)
discriminator = Discriminator(input_dim=3)
# Step 3: 训练 CF-GANs
criterion = nn.BCELoss()
g_optimizer = optim.Adam(generator.parameters(), lr=0.001)
d_optimizer = optim.Adam(discriminator.parameters(), lr=0.001)
for epoch in range(100):
for x_batch, t_batch, y_batch in train_loader:
# 训练判别器
real_labels = torch.ones(y_batch.size(0), 1)
fake_labels = torch.zeros(y_batch.size(0), 1)
d_optimizer.zero_grad()
real_loss = criterion(discriminator(x_batch, y_batch), real_labels)
fake_y = generator(x_batch, 1 - t_batch)
fake_loss = criterion(discriminator(x_batch, fake_y.detach()), fake_labels)
d_loss = real_loss + fake_loss
d_loss.backward()
d_optimizer.step()
# 训练生成器
g_optimizer.zero_grad()
g_loss = criterion(discriminator(x_batch, fake_y), real_labels)
g_loss.backward()
g_optimizer.step()
if epoch % 10 == 0:
print(f'Epoch {epoch}, D Loss: {d_loss.item():.4f}, G Loss: {g_loss.item():.4f}')
# Step 4: 生成反事实结果
def generate_counterfactuals(x, t):
t_cf = 1 - t # 反事实处理
return generator(torch.tensor(x, dtype=torch.float32), torch.tensor(t_cf, dtype=torch.float32).unsqueeze(1)).detach().numpy()
x_test = X[:5] # 取前5个样本
cf_outcomes = generate_counterfactuals(x_test, T[:5])
print("实际观察到的 Y:", Y[:5])
print("反事实生成的 Y:", cf_outcomes)
分析 CF-GANs 的执行步骤
数据生成:
我们模拟了1000名患者的特征(年龄、血压、体重)。 随机分配治疗T(0 或 1)。 定义了真实的未治疗和治疗后的健康状况 Y0,Y1。 观测值Y由T决定,即Y=T⋅Y1+(1−T)⋅Y0。
CF-GANs 训练:
- 生成器G生成反事实健康状况(即未观察到的治疗或非治疗结果)。
- 判别器D尝试区分真实观察值和生成器生成的反事实数据。
通过对抗训练,使得生成的反事实数据逼真。
反事实估计:
训练后,我们用CF-GANs生成某些患者的反事实健康状况。 例如,如果一个患者接受了治疗T=1,我们生成他未接受治疗T=0时的健康状况(反事实)。
ITE 计算:
通过计算ITE=Y1−Y0来估计个体治疗效应。
可视化
import matplotlib.pyplot as plt
import seaborn as sns
# 选取部分样本
num_samples = 50
x_test = X[:num_samples]
t_test = T[:num_samples]
y_test = Y[:num_samples]
cf_outcomes = generate_counterfactuals(x_test, t_test)
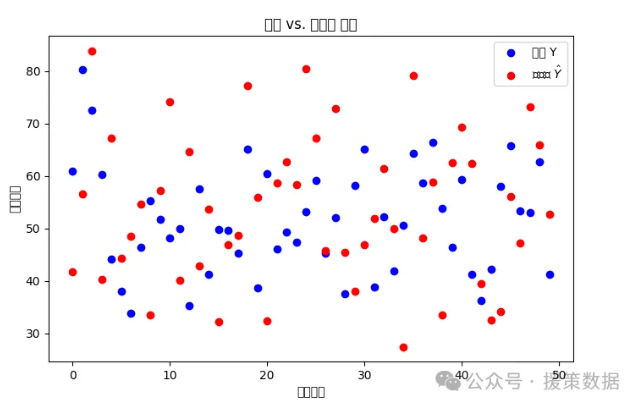
1. 真实 vs. 生成的反事实健康状况(散点图)
目标:比较观察到的健康状况Y和CF-GANs生成的反事实Y^。
图形:
横轴:患者索引(或个体特征)。 纵轴:健康评分Y。 用 蓝色点 表示观察到的Y(真实值)。 用 红色点 表示CF-GANs生成的反事实 Y^。 可连接真实和反事实点,以显示变化。
# 1. 真实 vs. 反事实散点图
plt.figure(figsize=(8, 5))
plt.scatter(range(num_samples), y_test, color='blue', label='真实 Y')
plt.scatter(range(num_samples), cf_outcomes, color='red', label='反事实 $\hat{Y}$')
plt.xlabel('样本索引')
plt.ylabel('健康评分')
plt.title('真实 vs. 反事实 评分')
plt.legend()
plt.show()
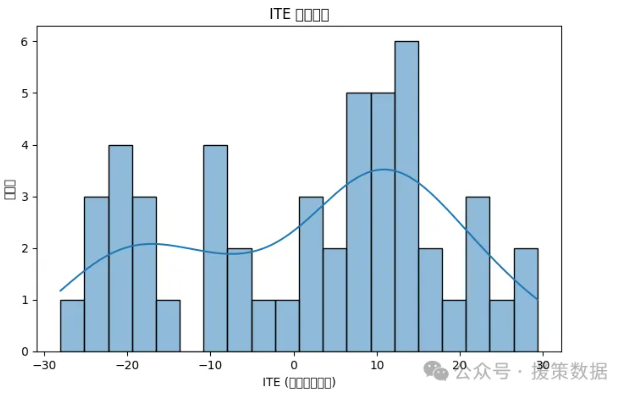
2. 个体治疗效应(ITE)分布图
目标:展示GANs生成的个体治疗效应(ITE)估计结果。
图形:
直方图或核密度估计图(KDE),展示ITE在总体上的分布情况。 直方图可观察不同个体对治疗的反应是否存在差异。
# 2. 个体治疗效应 ITE 分布
ITE = cf_outcomes.flatten() - y_test
plt.figure(figsize=(8, 5))
sns.histplot(ITE, bins=20, kde=True)
plt.xlabel('ITE (个体治疗效应)')
plt.ylabel('样本数')
plt.title('ITE 估计分布')
plt.show()
3. 真实 vs. 生成的分布比较(直方图)
目标:检查GANs生成的健康评分分布是否匹配真实数据分布。
图形:
画出 真实的Y(0)和Y(1)分布(蓝色)。 画出 CF-GANs 生成的Y^(0)和Y^(1)分布(红色)。 直方图叠加,若两个分布吻合,表示CF-GANs生成的反事实可靠。
# 3. 真实 vs. 生成分布对比
plt.figure(figsize=(8, 5))
sns.histplot(Y[T == 0], bins=20, kde=True, color='blue', label='真实 Y(0)', alpha=0.6)
sns.histplot(Y[T == 1], bins=20, kde=True, color='green', label='真实 Y(1)', alpha=0.6)
sns.histplot(cf_outcomes.flatten(), bins=20, kde=True, color='red', label='GAN 生成的反事实 $\hat{Y}$', alpha=0.6)
plt.xlabel('健康评分')
plt.ylabel('样本数')
plt.title('真实 vs. 生成的 Y 分布')
plt.legend()
plt.show()

可见,CF-GANs通过对抗训练学习数据分布,生成逼真的反事实结果,从而支持因果推断。这种方法在医疗、政策分析等领域具有广泛应用。








Comments NOTHING