1.汇编语言IEEE二进制浮点数表示
x86 处理器使用的三种浮点数二进制存储格式都是由 IEEE 标准 754-1985。二进制浮点数运算 (Standard 754-1985 for Binary Floating-Point Arithmetic) 所指定。
下表列出了它们的特点。
| 单精度 | 32 位:1 位符号位,8 位阶码,23 位为有效数字的小数部分。大致的规格化范围:2-126 〜2127 。也被称为短实数 (short real) |
| 双精度 | 64 位:1 位符号位,11 位阶码,52 位为有效数字的小数部分。大致的规格化范围:2-1022 〜21023 。也被称为长实数 (longreal) |
| 扩展双精度 | 80 位:1 位符号位,15 位阶码,1 位为整数部分,63 位为有效数字的小数部分。大致的规格化范围:2-16382〜216383。也被称为扩展实数 (extended real) |
由于三种格式比较相似,因此本节将重点关注单精度格式,如下图所示。32 位数值的最高有效位(MSB) 在最左边。标注为小数 (fraction) 的字段表示的是有效数字的小数部分。如同预想的一样,各个字节按照小端顺序(最低有效位 (LSB) 在起始地址上)存放在内存中。

1) 符号位
如果符号位为 1,则该数为负;如果符号位为 0,则该数为正。零被认为是正数。
2) 有效数字
在浮点数表达式 m*be 中,m 称为有效数字或尾数;b 为基数;e 为阶码。浮点数的有效数字(或尾数)由小数点左右的十进制数字构成。同样的概念也可以扩展到浮点数的小数部分。例如,十进制数 123.154 可以表示为下面的累加和形式:
123.154 = ( 1 X 102 ) + (2 X 101 ) + ( 3 X 100 ) + ( 1 X 10-1 ) + ( 5 X 10-6 )( 4 X 10-3 )
小数点左边数字的阶码都为正,右边数字的阶码都为负。
二进制浮点数也可以使用加权位计数法。浮点数十进制数值 11.1011 表示为:
11.1011 = (1 X 21 ) + (1 X 20 ) + (1 X 2-1 )( 0 X 2-2 ) + (1 X 2-3 ) + (1 X 2-4 )
小数点右边的数字还有一种表达方式,即将它们列为分数之和,其中分母为 2 的幂。上例的和为 11/16 ( 或 0.6875):
.1011 = 1/2+0/4+1/8+1/16=11/16
生成的小数部分非常直观。十进制分子 (11) 表示的就是二进制位组合 1011。如果小数点右边的有效位个数为 e 则十进制分母就为 2e :上例中,e=4,则有 2e=16。下表列出了更多的例子,来展示将二进制浮点数转换为以 10 为基数的分数。
| 二进制浮点数 | 基数为 10 的分数 | 二进制浮点数 | 基数为 10 的分数 |
|---|---|---|---|
| 11.11 | 3 3/4 | 0.00101 | 5/32 |
| 101.0011 | 5 3/16 | 1.011 | 1 3/8 |
| 1101.100101 | 13 37/64 | 0.00000000000000000000001 | 1/8388608 |
表中最后一项为 23 位规格化有效数字可以保存的最小分数。为便于参考,下表列出了二进制浮点数及其等价的十进制分数和十进制数值。
| 二进制 | 十进制分数 | 十进制数值 | 二进制 | 十进制分数 | 十进制数值 |
|---|---|---|---|---|---|
| .1 | 1/2 | .5 | .0001 | 1/16 | .0625 |
| .01 | 1/4 | .25 | .00001 | 1/32 | .03125 |
| .001 | 1/8 | .125 |
3) 有效数字的精度
用有限位数表示的任何浮点数格式都无法表示完整连续的实数。例如,假设一个简单的浮点数格式有 5 位有效数字,那么将无法表示范围在 1.1111〜10.000 之间的二进制数。比如,二进制数 1.11111 就需要更精确的有效数字。将这个思想扩展到 IEEE 双精度格式,就会发现其 53 位有效数字无法表示需要 54 位或更多位的二进制数值。
2.汇编语言阶码简介
单精度数用 8 位无符号整数存放阶码,引入的偏差为 127,因此必须在数的实际阶码上再加 127。考虑二进制数值 1.101 x 25 :将实际阶码 (5) 加上 127 后,形成的偏移码 (132) 保存到数据表示形式中。
下表给出了阶码的有符号十进制、偏移十进制,以及最后一列的无符号二进制。
| 阶码(E) | 偏移码(E+127) | 二进制 | 阶码(E) | 偏移码(E+127) | 二进制 |
|---|---|---|---|---|---|
| +5 | 132 | 10000100 | +127 | 254 | 11111110 |
| 0 | 127 | 01111111 | -126 | 1 | 00000001 |
| -10 | 117 | 01110101 | -1 | 126 | 01111110 |
偏移码总是正数,范围为 1〜254。如前所述,实际阶码的范围为 -126〜+127。这个经过选择的范围,使得最小可能阶码的倒数也不会发生溢出。
3.汇编语言规格化二进制浮点数
大多数二进制浮点数都以规格化格式 (normalized form) 存放,以便将有效数字的精度最大化。给定任意二进制浮点数,都可以进行规格化,方法是将二进制小数点移位,直到小数点左边只有一个“1”。
阶码表示的是二进制小数点向左(正阶码)或向右(负阶码)移动的位数。示例如下:
| 非规格化 | 规格化 |
|---|---|
| 1110.1 | 1.1101 X 23 |
| .000101 | 1.01 X 2-4 |
| 1010001. | 1.010001 x 26 |
反规格化数
规格化操作的逆操作是将二进制浮点数反规格化 (denormalize) ( 或非规格化 (unnormalize))。移动二进制小数点,直到阶码为 0。如果阶码为正数 n,则将二进制小数点右移 n 位;如果阶码为负数 n,则将二进制小数点左移 n 位,并在需要位置填充刖导数 0。
实数编码
一旦符号位、阶码和有效数字字段完成规格化和编码后,生成一个完整的二进制 IEEE 段实数就很容易了。首先将设置符号位,然后是阶码字段,最后是有效数字的小数部分。例如,下面表示的是二进制 1.101 x 20:
- 符号位:0
- 阶码:01111111
- 小数部分:10100000000000000000000
偏移码 (01111111) 是十进制数 127 的二进制形式。所有规格化有效数字在二进制小数点的左边都有个 1,因此,不需要对这一位进行显式编码。更多的例子参见下表。
| 二进制数值 | 偏移阶码 | 符号、阶码、小数部分 |
|---|---|---|
| -1.11 | 127 | 1 01111111 11000000000000000000000 |
| +1101.101 | 130 | 0 10000010 10110100000000000000000 |
| -.00101 | 124 | 1 0111110001000000000000000000000 |
| +100111.0 | 132 | 0 10000100 00111000000000000000000 |
| +.0000001101011 | 120 | 001111000 10101100000000000000000 |
IEEE 规范包含了多种实数和非数字编码。
- 正零和负零
- 非规格化有限数
- 规格化有限数
- 正无穷和负无穷
- 非数字 (NaN,即不是一个数字 (Not a Number))
- 不定数
不定数被浮点单元 (FPU) 用于响应一些无效的浮点操作。
规格化和非规格化
规格化有限数 (nonnalized finite numbers) 是指所有非零有限值,这些数能被编码为零到无穷之间的规格化实数。尽管看上去全部有限非零浮点数都应被规格化,但是若数值接近于零,则无法规格化。
当阶码范围造成的限制使得 FPU 不能将二进制小数点移动到规格化位置时,就会发生这种情况。假设 FPU 计算结果为 1.0101111 x 2-129。
其阶码太小,无法用单精度数形式存放。此时产生一个下溢异常,数值则每次将二进制小数点左移一位逐步进行非规格化,直到阶码达到有效范围:
1.01011110000000000001111 x 2-129
0.10101111000000000000111 X 2-128
0.01010111100000000000011 x 2-127
0.00101011110000000000001 x 2-126
在这个例子中,移动二进制小数点导致有效数字损失了精度。
正无穷和负无穷
正无穷 (+∞) 表示最大正实数,负无穷 (-∞) 表示最大负实数。无穷可以与其他数值比较:-∞ 小于 +∞,-∞ 小于任意有限数,+∞ 大于任意有限数。任一无穷都可以表示浮点溢出条件。运算结果不能规格化的原因是,结果的阶码太大而无法用有效阶码位数来表示。
NaN
NaN 是不表示任何有效实数的位模式。x86 有两种 NaN:quiet NaN 能够通过大多数算术运算来传递,而不会引起异常。signaling NaN 则被用于产生一个浮点无效操作异常。
编译器可以用 signaling NaN 填充未初始化数组,那么,任何试图在这个数组上执行的运算都会引发异常。quiet NaN 可以用于存在调试期间生成的诊断信息。程序可根据需要自由地在 NaN 中编入任何信息。FPU 不会尝试在 NaN 上执行操作。Intel 手册有一组规则确定了以这两种 NaN 为操作数的指令结果。
特定编码
在浮点运算中,常常会出现一些特定的数值编码,如下表所示。字母 x 表示的位,其值可以为 1,也可以为 0。 QNaN 是 quiet NaN, SNaN 是 signaling NaN。
| 数值 | 符号、阶码、有效数字 |
|---|---|
| Positive zero | 0 00000000 00000000000000000000000 |
| Negative zero | 1 00000000 00000000000000000000000 |
| Positive infinity | 0 11111111 00000000000000000000000 |
| Negative infinity | 1 11111111 00000000000000000000000 |
| QNaN | x 11111111 1xxxxxxxxxxxxxxxxxxxxxx |
| SNaN | x 11111111 0xxxxxxxxxxxxxxxxxxxxxx |
4.汇编语言十进制小数转换为二进制实数
当十进制小数可以表示为形如 (1/2+1/4+1/8+…) 的分数之和时,发现与之对应的二进制实数就非常容易了。如下表所示,左列中的大多数分数不容易转换为二进制。不过,可以将它们写成第二列的形式。
| 十进制分数 | 分解为… | 二进制实数 | 十进制分数 | 分解为… | 二进制实数 |
|---|---|---|---|---|---|
| 1/2 | 1/2 | .1 | 3/8 | 1/4+1/8 | .011 |
| 1/4 | 1/4 | .01 | 1/16 | 1/16 | .0001 |
| 3/4 | 1/2+1/4 | .11 | 3/16 | 1/8+1/16 | .0011 |
| 1/8 | 1/8 | .001 | 5/16 | 1/4+1/16 | .0101 |
| 7/8 | 1/2+1/4+1/8 | .111 |
很多实数,如 1/10(0.1)或 1/100(0.01),不能表示为有限位的二进制数,它们只能近似地表示为一组以 2 的幂为分母的分数之和。想想看,像 $39.95 这样的货币值受到了怎样的影响!
使用二进制长除法
当十进制数比较小的时候,将十进制分数转换为二进制的一个简单方法就是:先将分子与分母转换为二进制,再执行长除。例如,十进制数 0.5 表示为分数就是 5/10,那么十进制 5 等于二进制 0101,十进制 10 等于二进制 1010。执行了长除之后,商为二进制数 0.1:

当被除数减去除数 1010 的结果为 0 时,除法完成。因此,十进制分数 5/10 等于二进制数 0.1。这种方法被称为二进制长除法(binary long division method)。
下面用二进制长除法将十进制数 0.2(2/10)转换为二进制数。首先,用二进制 10 除以二进制 1010(十进制 10):

第一个足够大到能上商的数是 10000。从 10000 减去 1010 后,余数为 110。添加一个 0 后,形成新的被除数 1100。从 1100 减去 1010 后,余数为 10。添加三个 0 后,形成新的被除数 10000。
这个数与第一个被除数相同。从这里开始,商的位序列出现重复(0011…),由此可知,不会得到确定的商,所以,0.2 也不能表示为有限位的数。其单精度编码的有效数字为 10011001100110011001100。
单精度数转换为十进制
IEEE 单精度数转换为十进制时,建议步骤如下:
1) 若 MSB 为 1,该数为负;否则,该数为正。
2) 其后 8 位为阶码。从中减去二进制值 01111111(十进制数 127),生成无偏差阶码。将无偏差阶码转换为十进制。
3) 其后 23 位表示有效数字。添加“1.”,后面紧跟有效数字位,尾随零可以忽略。用形成的有效数字、第一步得到的符号和第二步计算出来的阶码,就构成一个二进制浮点数。
4) 对第三步生成的二进制数进行非规格化。(按照阶码的值移动二进制小数点。如果阶码为正,则右移;如果阶码为负,则左移。)
5) 利用加权位计数法,从左到右,将二进制浮点数转换为 2 的幂之和,形成十进制数。
【示例】IEEE(0 10000010 01011000000000000000000)转换为十进制
1) 该数为正数。
2) 无偏差阶码的二进制值为 00000011,十进制值为 3。
3) 将符号、阶码和有效数字组合起来即得该二进制数为 +1.01011 x2³。
4) 非规格化二进制数为 +1010.11。
5) 则该数的十进制值为 +10 3/4,或 +10.75。
5.汇编语言FPU寄存器栈(register stack)
FPU 不使用通用寄存器 (EAX、EBX 等等)。反之,它有自己的一组寄存器,称为寄存器栈 (register stack)。数值从内存加载到寄存器栈,然后执行计算,再将堆栈数值保存到内存。
FPU 指令用后缀 (postfix) 形式计算算术表达式,这和惠普计算器的方法大致相同。比如,现有一个中缀表达式 (infix expression):(5*6)+4,其后缀表达式为:
5 6 * 4 +
中缀表达式 (A+B)*C 要用括号来覆盖默认的优先级规则(乘法在加法之前)。与之等效的后缀表达式则不需要括号:
A B + C *
表达式堆栈
在计算后缀表达式的过程中,用堆栈来保存中间结果。下图展示了计算后缀表达式 56*4- 所需的步骤。堆栈条目被标记为 ST(0) 和 ST(1),其中 ST(0) 表示堆栈指针通常所指位置。

中缀表达式转换为后缀表达式的常见方法在互联网以及计算机科学入门读物中都可以查阅到,此处不再赘述。下表给岀了一些等价表达式。
| 中缀 | 后缀 | 中缀 | 后缀 |
|---|---|---|---|
| A+B | AB+ | (A+B)*(C+D) | AB+CD+* |
| (A-B)/D | AB-D/ | ((A+B)/C)*(E—F) | AB+C/EF-* |
FPU 数据寄存器
FPU 有 8 个独立的、可寻址的 80 位数据寄存器 R0〜R7,如下图所示,这些寄存器合称为寄存器栈。FPU 状态字中名为 TOP 的一个 3 位字段给出了当前处于栈顶的寄存器编号。例如,在下图中,TOP 等于二进制数 011,这表示栈顶为 R3。在编写浮点指令时,这个位置也称为 ST(0)(或简写为 ST)。最后一个寄存器为 ST(7)。

如同所想的一样,入栈(push)操作(也称为加载)将 TOP 减 1,并把操作数复制到标识为 ST(0) 的寄存器中。如果在入栈之前,TOP 等于 0,那么 TOP 就回绕到寄存器 R7。
出栈(pop)操作(也称为保存)把 ST(0) 的数据复制到操作数,再将TOP加1。如果在出栈之前,TOP 等于 7,则 TOP 就回绕到寄存器 R0。
如果加载到堆栈的数值覆盖了寄存器栈内原有的数据,就会产生一个浮点异常(floating-point exception)。下图展示了数据 1.0 和 2.0 入栈后的堆栈情况。

尽管理解 FPU 如何用一组有限数量的寄存器实现堆栈很有意思,但这里只需关注 ST(n),其中 ST(0) 总是表示栈顶。从这里开始,引用栈寄存器时将使用 ST(0),ST(1),以此类推。指令操作数不能直接引用寄存器编号。
寄存器中浮点数使用的是 IEEE 10 字节扩展实数格式(也被称为临时实数(temporary real))。当 FPU 把算术运算结果存入内存时,它会把结果转换成如下格式之一:整数、长整
数、单精度(短实数)、双精度(长实数),或者压缩二进制编码的十进制数(BCD)。
专用寄存器
FPU 有 6 个专用(special-purpose)寄存器,如下图所示:

- 操作码寄存器:保存最后执行的非控制指令的操作码。
- 控制寄存器:执行运算时,控制精度以及 FPU 使用的舍入方法。还可以用这个寄存器来屏蔽(隐藏)单个浮点异常。
- 状态寄存器:包含栈顶指针、条件码和异常警告。
- 标识寄存器:指明 FPU 数据寄存器栈内每个寄存器的内容。其中,每个寄存器都用两位来表示该寄存器包含的是一个有效数、零、特殊数值 (NaN、无穷、非规格化,或不支持的格式 ),还是为空。
- 最后指令指针寄存器:保存指向最后执行的非控制指令的指针。
- 最后数据(操作数)指针寄存器:保存指向数据操作数的指针,如果存在,那么该数被最后执行的指令所使用。
操作系统使用这些专用寄存器在任务切换时保存状态信息。
6.汇编语言FPU舍入:计算浮点数的精确结果
FPU 尝试从浮点计算中产生非常精确的结果。但是,在很多情况下这是不可能的,因为目标操作数可能无法精确表示计算结果。比如,假设现有一特定存储格式只允许 3 个小数位。那么,该格式可以保存形如 1.011 或 1.101 的数值,而不能保存形如 1.0101 的数值。
若计算的精确结果为 +1.0111 (十进制数 1.4375),那么,既可以通过加 0.0001 向上舍入该数,也可以通过减 0.0001 向下舍入:
(a) 1.0111 -> 1.100
(b) 1.0111 -> 1.011
若精确结果是负数,那么加 -0.0001 会使舍入结果更接近 -∞。而减去 -0.0001 会使舍入结果更接近 0 和 +8:
(a) -1.0111 -> -1.100
(b) -1.0111 -> -1.011
FPU 可以在四种舍入方法中进行选择:
1) 舍入到最接近的偶数 (round to nearest even):舍入结果最接近无限精确的结果。如果有两个值近似程度相同,则取偶数值 (LSB=0)。
2) 向 -∞ 舍入 (round down to -∞ ):舍入结果小于或等于无限精确结果。
3) 向 +∞ 舍入 (round down to +∞ ):舍入结果大于或等于无限精确结果。
4) 向 0 舍入 (round toward zero):也被称为截断法,舍入结果的绝对值小于或等于无限精确结果。
FPU 控制字
FPU 控制字用两位指明使用的舍入方法,这两位被称为 RC 字段,字段数值(二进制)如下:
- 00:舍入到最接近的偶数(默认)。
- 01:向负无穷舍入。
- 10:向正无穷舍入。
- 11:向 0 舍入(截断)。
舍入到最接近的偶数是默认选择,它被认为是最精确的,也最适合大多数应用程序。下表以二进制数 +1.0111 为例,展示了四种舍入方法。
| 方法 | 精确结果 | 舍入结果 | 方法 | 精确结果 | 舍入结果 |
|---|---|---|---|---|---|
| 舍入到最接近的偶数 | 1.0111 | 1.100 | 向 +∞ 舍入 | 1.0111 | 1.100 |
| 向 -∞ 舍入 | 1.0111 | 1.011 | 向 0 舍入 | 1.0111 | 1.011 |
同样,下表展示了二进制数 -1.0111 的舍入结果。
7.汇编语言浮点数异常与常用指令集
每个程序都可能出错,而 FPU 就需要处理这些结果。因而,它要识别并检测 6 种类型的异常条件:
- 无效操作(#I)
- 除零(#Z)
- 非规格化操作数(#D)
- 数字上溢(#O)
- 数字下溢(#U)
- 模糊精度(#P)
前三个(#I、#Z 和 #D)在全部运算操作发生前进行检测,后三个(#O、#U 和 #P)则在操作发生后检测。
每种异常都有对应的标志位和屏蔽位。当检测到浮点异常时,处理器将与之匹配的标志位置 1。每个被处理器标记的异常都有两种可能的操作:
- 如果相应的屏蔽位置 1,那么处理器自动处理异常并继续执行程序。
- 如果相应的屏蔽位清 0,那么处理器将调用软件异常处理程序。
大多数程序普遍都可以接受处理器的屏蔽(自动)响应。如果应用程序需要特殊响应,那么可以使用自定义异常处理程序。一条指令能触发多个异常,因此处理器要持续保存自上一次异常清零后所发生的全部异常。完成一系列计算后,可以检测是否发生了异常。
浮点数指令集
FPU 指令集有些复杂,因此这里只对其功能进行概述,并用具体例子给出编译器通常会生成的代码。此外,大家还将看到如何通过改变舍入模式来控制 FPU。指令集包括如下基本指令类型:
- 数据传送
- 基本算术运算
- 比较
- 超越函数
- 常数加载(仅对专门预定义的常数)
- x87 FPU 控制
- x87 FPU 和 SIMD 状态管理
浮点指令名用字母 F 开头,以区别于 CPU 指令。指令助记符的第二个字母(通常为 B 或 I)指明如何解释内存操作数:B 表示 BCD 操作数,I 表示二进制整数操作数。
如果这两个字母都没有使用,则内存操作数将被认为是实数。比如,FBLD 操作对象为 BCD 数值, FILD 操作对象为整数,而 FLD 操作对象为实数。
操作数
浮点指令可以包含零操作数、单操作数和双操作数。如果是双操作数,那么其中一个必然为浮点寄存器。指令中没有立即操作数,但是某些预定义常数(如 0.0,π 和 log210)可以加载到堆栈。
通用寄存器 EAX、EBX、ECX 和 EDX 不能作为操作数。(唯一的例外是 FSTSW,它将 FPU 状态字保存在 AX 中。)不允许内存-内存操作。
整数操作数从内存(不是从 CPU 寄存器)加载到 FPU,并自动转换为浮点格式。同样,将浮点数保存到整数内存操作数时,该数值也会被自动截断或舍入为整数。
初始化(FINIT)
FINIT 指令对 FPU 进行初始化。将 FPU 控制字设置为 037Fh,即屏蔽(隐藏)了所有浮点异常;舍入模式设置为最近偶数,计算精度设置为 64 位。建议在程序开始时调用 FINIT, 这样就可以了解处理器的起始状态。
浮点数据类型
现在快速回顾一下 MASM 支持的浮点数据类型(QWORD、TBYTE、REAL4、REAL8 和 REAL10),如下表所示。
| 类型 | 用法 |
|---|---|
| QWORD | 64 位整数 |
| TBYTE | 80 位(10 字节)整数 |
| REAL4 | 32 位(4 字节)IEEE 短实数 |
| REAL8 | 64 位(8 字节)IEEE 长实数 |
| REAL10 | 80 位(10 字节)IEEE 扩展实数 |
在定义 FPU 指令 的内存操作数时,将会使用到这些类型。例如,加载一个浮点变量到 FPU 堆栈,这个变量可以定义为 REAL4,REAL8 或 REAL10:
.data
bigVal REAL10 1.212342342234234243E+864
.code
fld bigVal ;加载变量到堆栈
加载浮点数值(FLD)
FLD(加载浮点数值)指令将浮点操作数复制到 FPU 堆栈栈顶(称为 ST(0))。操作数可以是 32 位、64 位、80 位的内存操作数(REAL4、REAL8、REAL10)或另一个 FPU 寄存器:
FLD m32fp
FLD m64fp
FLD m80fp
FLD ST(i)
内存操作数类型 FLD 支持的内存操作数类型与 MOV 指令一样。示例如下:
.data
array REAL8 10 DUP (?)
.code
fid array ;直接寻址
fid [array+16 ] ;直接偏移
fid REAL8 PTR[esi] ;间接寻址
fid array[esi] ;变址寻址
fid array[esi*8] ;带比例因子的变址
fid array[esi*TYPE array] ;带比例因子的变址
fid REAL8 PTR[ebx+esi] ;基址-变址
fid array[ebx+esi] ;基址-变址-偏移量
fid array[ebx+esi*TYPE array] ;带比例因子的基址-变址-偏移量
【示例】下面的例子加载两个直接操作数到 FPU 堆栈:
.data
dblOne REAL8 234.56
dblTwo REAL8 10.1
.code
fid dblOne ; ST(0) = dblOne
fid dblTwo ; ST(0) = dblTwo, ST(1) = dblOne
每条指令执行后的堆栈情况如下图所示:

执行第二条 FLD 时,TOP 减 1,这使得之前标记为 ST(0) 的堆栈元素变为了 ST(1)。
FILD
FILD(加载整数)指令将 16 位、32 位或 64 位有符号整数源操作数转换为双精度浮点数,并加载到 ST(0)。源操作数符号保留。FILD 支持的内存操作数类型与 MOV 指令一致(间接、变址、基址-变址等)。
加载常数
下面的指令将特定常数加载到堆栈。这些指令没有操作数:
- FLD1 指令将 1.0 压入寄存器堆栈。
- FLDL2T 指令将 log210 压入寄存器堆栈。
- FLDL2E 指令将 log2e 压入寄存器堆栈。
- FLDPI 指令将 π 压入寄存器堆栈。
- FLDLG2 指令将 log102 压入寄存器堆栈。
- FLDLN2 指令将 loge2压入寄存器堆栈。
- FLDZ(加载零)指令将 0.0 压入 FPU 堆栈。
保存浮点数值(FST, FSTP)
FST(保存浮点数值)指令将浮点操作数从 FPU 栈顶复制到内存。FST 支持的内存操作数类型与 FLD 一致。操作数可以为 32 位、64 位、80 位内存操作数(REAL4、REAL8、 REAL10)或另一个 FPU 寄存器:
FST m32fp FST m80fp
FST m64fp FST ST(i)
FST 不是弹出堆栈。下面的指令将 ST(0) 保存到内存。假设 ST(0) 等于 10.1,ST(1) 等于 234.56:
fst dblThree ; 10.1
fst dblFour ; 10.1
直观地说,代码段期望 dblFour 等于 234.56。但是第一条 FST 指令把 10.1 留在 ST(0) 中。如果代码段的意图是把 ST(1) 复制到 dblFour,那么就要用 FSTP 指令。
FSTP
FSTP(保存浮点值并将其出栈)指令将 ST(0) 的值复制到内存并将 ST(0) 弹出堆栈。假设执行下述指令前 ST(0) 等于 10.1,ST(1) 等于 234.56:
fstp dblThree ; 10.1
fstp dblFour ; 234.56
指令执行后,这两个数值会从堆栈中逻辑移除。从物理上看,每次执行 FSTP,TOP 指针都会减 1,修改 ST(0) 的位置。
FIST(保存整数)指令将 ST(0) 的值转换为有符号整数,并把结果保存到目标操作数。保存的值可以为字或双字。FIST 支持的内存操作数类型与 FST 一致。
8.汇编语言浮点数算术运算指令
下表列出了基本算术运算操作。所有算术运算指令支持的内存操作数类型与 FLD (加载)和 FST(保存)一致,因此,操作数可以是间接操作数、变址操作数和基址-变址操作数等等。
| FCHS | 修改符号 |
| FADD | 源操作数与目的操作数相加 |
| FSUB | 从目的操作数中减去源操作数 |
| FSUBR | 从源操作数中减去目的操作数 |
| FMUL | 源操作数与目的操作数相乘 |
| FDIV | 目的操作数除以源操作数 |
| FDIVR | 源操作数除以目的操作数 |
FCHS 和 FABS
FCHS( 修改符号 ) 指令将 ST(0) 中浮点数值的符号取反。FABS ( 绝对值 ) 指令清除 ST(0) 中数值的符号,以得到它的绝对值。这两条指令都没有操作数:
FCHS
FABS
FADD、FADDP、FIADD
FADD(加法)指令格式如下,其中,m32fp 是 REAL4 内存操作数,m64fp 即是 REAL8 内存操作数,i 是寄存器编号:
FADD
FADD m32fp
FADD m64fp
FADD ST(0), ST(i)
FADD ST(i) , ST(0)
无操作数
如果 FADD 没有操作数,则 ST(0)与 ST(1)相加,结果暂存在 ST(l)。然后 ST(0) 弹出堆栈,把加法结果保留在栈顶。假设堆栈已经包含了两个数值,下图展示了 FADD 的操作:

寄存器操作数
从同样的栈开始,如下所示将 ST(0) 加到 ST(1):

内存操作数
如果使用的是内存操作数,FADD 将操作数与 ST(0) 相加。示例如下:
fadd mySingle ; ST(0) += mySingle
fadd REAL8 PTR[esi] ; ST(0) += [esi]
FADDP
FADDP(相加并出栈)指令先执行加法操作,再将 ST(0) 弹出堆栈。MASM 支持如下格式:
FADDP ST(i),ST(0)
下图演示了 FADDP 的操作过程:

FIADD
FIADD(整数加法)指令先将源操作数转换为扩展双精度浮点数,再与 ST(0) 相加。指令语法如下:
FIADD ml6int
FIADD m32int
示例:
.data
myInteger DWORD 1
.code
fiadd myInteger ; ST(0) += myInteger
FSUB、FSUBP、FISUB
FSUB 指令从目的操作数中减去源操作数,并把结果保存在目的操作数中。目的操作数总是一个 FPU 寄存器,源操作数可以是 FPU 寄存器或者内存操作数。该指令操作数类型与 FADD 指令一致:
FSUB
FSUB m32fp
FSUB m64fp
FSUB ST(0), ST(i)
FSUB ST(i), ST(0)
FSUB 的操作与 FADD 相似,只不过它进行的是减法而不是加法。比如,无参数 FSUB 实现 ST(1) – ST(0),结果暂存于 ST(1)。然后 ST(0) 弹出堆栈,将减法结果留在栈顶。若 FSUB 使用内存操作数,则从 ST(0) 中减去内存操作数,且不再弹出堆栈。
fsub mySingle ; ST(0) -= mySingle
fsub array[edi*8] ; ST(0) -= array[edi*8]
FSUBP
FSUBP(相减并出栈)指令先执行减法,再将 ST(0) 弹出堆栈。MASM 支持如下格式:
FSUBP ST(i),ST(0)
FISUB
FISUB(整数减法)指令先把源操作数转换为扩展双精度浮点数,再从 ST(0) 中减去该操作数:
FISUB m16int
FISUB m32int
FMUL、FMULP、FIMUL
FMUL 指令将源操作数与目的操作数相乘,乘积保存在目的操作数中。目的操作数总是一个 FPU 寄存器,源操作数可以为寄存器或者内存操作数。其语法与 FADD 和 FSUB 相同:
FMUL
FMUL m32fp
FMUL m64fp
FMUL ST(0), ST(i)
FMUL ST(i), ST(0)
除了执行的是乘法而不是加法外,FMUL 的操作与 FADD 相同。比如,无参数 FMUL 将 ST(O) 与 ST(1) 相乘,乘积暂存于 ST(1)。然后 ST(0) 弹出堆栈,将乘积留在栈顶。同样,使用内存操作数的 FMUL 则将内存操作数与 ST(0) 相乘:
fmul mySingle ; ST(0) *= mySingle
FMULP
FMULP(相乘并出栈)指令先执行乘法,再将 ST(0) 弹出堆栈。MASM 支持如下格式:
FMULP ST(i),ST(O)
FIMUL 与 FIADD 相同,只是它执行的是乘法而不是加法:
FIMUL ml6int
FIMUL m32int
FDIV、FDIVP、FIDIV
FDIV 指令执行目的操作数除以源操作数,被除数保存在目的操作数中。目的操作数总是一个寄存器,源操作数可以为寄存器或者内存操作数。其语法与 FADD 和 FSUB 相同:
FDIV
FDIV m32fp
FDIV m64fp
FDIV ST(O), ST(i)
FDIV ST(i), ST(O)
除了执行的是除法而不是加法外,FDIV 的操作与 FADD 相同。比如,无参数 FDIV 执行 ST(1) 除以 ST(0)。然后 ST(0) 弹出堆栈,将被除数留在栈顶。使用内存操作数的 FDIV 将 ST(0) 除以内存操作数。下面的代码将 dblOne 除以 dblTwo,并将商保存到 dblQuot:
.data
dblOne REAL8 1234.56
dblTwo REAL8 10.0
dblQuot REAL8 ?
.code
fid dblOne ; 加载到 ST (0)
fdiv dblTwo ; ST(0) 除以 dblTwo
fstp dblQuot ; 将 ST(0) 保存到 dblQuot
若源操作数为 0,则产生除零异常。若源操作数等于正、负无穷,零或 NaN,则使用一些特殊情况。
FIDIV
FIDIV 指令先将整数源操作数转换为扩展双精度浮点数,再执行与 ST(0) 的除法。其语法如下:
FIDIV ml6int
FIDIV m32int
9.汇编语言FCOM指令:比较浮点数值
浮点数不能使用 CMP 指令进行比较,因为后者是通过整数减法来执行比较的。取而代之,必须使用 FCOM 指令。
执行 FCOM 指令后,还需要采取特殊步骤,然后再使用逻辑 IF 语句中的条件跳转指令(JA、JB、JE 等)。由于所有的浮点数都为隐含的有符号数,因此,FCOM 执行的是有符号比较。
FCOM、FCOMP、FCOMPP
FCOM(比较浮点数)指令将其源操作数与 ST(0) 进行比较。源操作数可以为内存操作数或 FPU 寄存器。其语法如下表所示:
| 指令 | 说明 |
|---|---|
| FCOM | 比较 ST(0) 与 ST(1) |
| FCOM m32fp | 比较 ST(0) 与 m32fp |
| FCOM m64fp | 比较 ST(0) 与 m64fp |
| FCOM ST(i) | 比较 ST(0) 与 ST(i) |
FCOMP 指令的操作数类型和执行的操作与 FCOM 指令相同,但是它要将 ST(0) 弹岀堆栈。FCOMPP 指令与 FCOMP 相同,但是它有两次出栈操作。
条件码
FPU 条件码标识有 3 个,C3、C2 和 C0,用以说明浮点数比较的结果,如下表所示。由于 C3、C2 和 C0 的功能分别与零标志位 (ZF)、奇偶标志位 (PF) 和进位标志位 (CF) 相同,因此表中列标题给出了与之等价的 CPU 状态标识。
| 条件 | C3(零标志位) | C2(奇偶标志位) | C0(进位标志位) | 使用的条件跳转指令 |
|---|---|---|---|---|
| ST(0) > SPC | 0 | 0 | 0 | JA.JNBE |
| ST(0) < SPC | 0 | 0 | 1 | JB.JNAE |
| ST(0) = SPC | 1 | 0 | 0 | JE.JZ |
| 无序 | 1 | 1 | 1 | (无) |
提示:如果出现无效算术运算操作数异常(无效操作数),且该异常被屏蔽,则 C3、C2 和 C0 按照标记为“无序”的行来设置。
在比较了两个数值并设置了 FPU 条件码之后,遇到的主要挑战就是怎样根据条件分支到相应标号。这包括了两个步骤:
- 用 FNSTSW 指令把 FPU 状态字送入 AX。
- 用 SAHF 指令把 AH 复制到 EFLAGS 寄存器。
条件码送入 EFLAGS 之后,就可以根据 ZF、PF 和 CF 进行条件跳转。上表列出了每种标志位组合所对应的条件跳转。根据该表还可以推出其他跳转:如果 CF=0,则可以使用 JAE 指令引发控制转移;如果 CF=1 或 ZF=1,则可使用 JBE 指令引发控制转移;如果 ZF=0,则可使用 JNE 指令。
【示例】现有如下 C++ 代码段:
double X = 1.2;
double Y = 3.0;
int N = 0;
if( X < Y )
N = 1;
与之等效的汇编语言代码如下:
.data
X REAL8 1.2
Y REAL8 3.0
N DWORD 0
.code
if( X < Y )
; N = 1
fid X ; ST(0) = X
fcomp Y ;比较 ST (0)和 Y
fnstsw ax ;状态字送入AX
sahf ;AH 复制至!) EFLAGS
jnb L1 ;X不小于Y?跳过
mov Nz1 ; N = 1
L1:
P6 处理器的改进
对上面的例子需要说明一点的是浮点数比较的运行时开销大于整数比较。考虑到这一点,Intel P6 系列引入了 FCOMI 指令。该指令比较浮点数值,并直接设置 ZF、PF 和 CF。P6 系列以 Pentium Pro 和 Pentium II 处理器为起点。) FCOMI 的语法如下:
FCOMI 指令代替了之前代码段中的三条指令,但是增加了一条 FLD 指令。FCOMI 指令不使用内存操作数。
相等比较
几乎所有的编程入门教材都会警告读者不要进行浮点数相等的比较,其原因是在计算
过程中出现的舍入误差。现在通过计算表达式 (sqrt(2.0)*sqrt(2.0)) -2.0 来对这个问题进行说明。从数学上看,这个表达式应 该等于0,但计算结果却相差甚远(约等于 4.4408921E-016)。 使用如下数据,下表列出了每一步计算后FPU堆栈的情况:
vail REAL8 2.0
| 指令 | FPU堆栈 |
|---|---|
| fidvall | ST(0) : +2.0000000E+000 |
| fsqrt | ST(0) : +1.4142135E+000 |
| fmul | ST(0), ST(0) ST(0) : +2.0000000E+000 |
| fsub vail | ST(0) : +4.4408921E-016 |
比较两个浮点数 n 和 y 的正确方法是取它们差值的绝对值|x-y|,再将其与用户定义的误差值 epsilon 进行比较。汇编语言代码如下,其中,epsilon 为两数差值允许的最大值,不 大于该值则认为这两个浮点数相等:
.data
epsilon REAL8 1.0E-12
val2 REAL8 0.0 ;比较的数值
val3 REAL8 1.01E —13 ;认为等于^&丄2
.code
;如果 (val2 == val3 ),显示”Values are equal”.
fid epsilon
fid val2
fsu val3
fabs
fcomi ST(0)ZST(1)
ja skip
mWrite <“Values are equal”,Odh,0ah>
skip:
下表跟踪程序执行过程,显示了前四条指令执行后的堆栈情况。
| 指令 | FPU堆栈 | 指令 | FPU堆栈 |
|---|---|---|---|
| fid epsilon | ST(0): +1.0000000E-012 | ST(1): +1.0000000E-012 | |
| fid val2 | ST(0): +0.0000000E+000 | fabs | ST(0): +1.0010000E-013 |
| ST(1): +1.0000000E-012 | ST(1): +1.0000000E-012 | ||
| fsub val3 | ST(0): -1.0010000E-013 | fcomi ST(0), ST(1) | ST(0)<ST(1), so CF=1, ZF=0 |
如果将 val3 重新定义为大于 epsilon,它就不会等于 val2:
val3 REAL8 1.001E-12 ;不相等
10.汇编语言读写浮点数值
本教程链接库有两个浮点数输入输出过程,如下所示:
- ReadFloat:从键盘读取一个浮点数,并将其压入浮点堆栈。
- WriteFloat:将 ST(0) 中的浮点数以阶码形式写到控制台窗口。
ReadFloat 接收各种形式的浮点数,示例如下:
35
+35.
-3.5
.35
3.5E5
3.5E005
-3.5E+5
3.5E-4
+3.5E-4
ShowFPUStack 另一个有用的过程,能够显示 FPU 堆栈。调用该过程不需要参数:
call ShowFPUStack
【示例】下面的示例程序把两个浮点数压入 FPU 堆栈并显示,再由用户输入两个数,将它们相乘并显示乘积:
; 32位浮点数 I/O 测试 (floatTest32.asm)
INCLUDE Irvine32.inc
INCLUDE macros.inc
.data
first REAL8 123.456
second REAL8 10.0
third REAL8 ?
.code
main PROC
finit ; 初始化 FPU
; 两个浮点数入栈,并显示 FPU 堆栈.
fld first
fld second
call ShowFPUStack
; 输入两个浮点数,并显示它们的乘机
mWrite "Please enter a real number: "
call ReadFloat
mWrite "Please enter a real number: "
call ReadFloat
fmul ST(0),ST(1) ; 相乘
mWrite "Their product is: "
call WriteFloat
call Crlf
exit
main ENDP
END main
示例输入/输出(用户输入显示为粗体)如下:

11.汇编语言FWAIT(WAIT)指令:异常同步
整数 (CPU) 和 FPU 是相互独立的单元,因此,在执行整数和系统指令的同时可以执行浮点指令。这个功能被称为并行性 (concurrency),当发生未屏蔽的浮点异常时,它可能是个潜在的问题。反之,已屏蔽异常则不成问题,因为,FPU 总是可以完成当前操作并保存结果。
发生未屏蔽异常时,中断当前的浮点指令,FPU 发异常事件信号。当下一条浮点指令或 FWAIT(WAIT) 指令将要执行时,FPU 检查待处理的异常。如果发现有这样的异常,FPU 就调用浮点异常处理程序(子程序)。
如果引发异常的浮点指令后面跟的是整数或系统指令,情况又会是怎样的呢?很遗憾,指令不会检查待处理异常,它们会立即执行。假设第一条指令将其输出送入一个内存操作数,而第二条指令又要修改同一个内存操作数,那么异常处理程序就不能正确执行。示例如下:
.data
intVal DWORD 25
.code
fild intVal ;将整数加载到 ST(0)
inc intVal ;整数加 1
设置 WAIT 和 FWAIT 指令是为了在执行下一条指令之前,强制处理器检查待处理且未屏蔽的浮点异常。这两条指令中的任一条都可以解决这种潜在的同步问题,直到异常处理程序结束,才执行 INC 指令。
fild intVal ;将整数加载到 ST(0)
fwait ;等待待处理异常
inc intVal ;整数加 1
下面将用几个简短的例子来演示浮点算术运算指令。一个很好的学习方法是用 C++ 编写表达式,编译后,再检查由编译器生成的代码。
表达式
现在编写代码,计算表达式 valD=-valA+(valB*valC)。下面给出一种可能的循序渐进的方法:将 valA 加载到堆栈,并取其负数;将 valB 加载到 ST(0),则 valA 成为 ST(1);将 ST(0) 和 valC 相乘,乘积保存在 ST(0) 中;将 ST(1) 与 ST(0) 相加,和数保存到 valD:
.data
valA REAL8 1.5
valB REAL8 2.5
valC REAL8 3.0
valD REAL8 ?; +6.0
.code
fld valA ; ST(0) = valA
fchs ;修改 ST(0) 的符号
fld valB ; 将 valB 加载到 ST(0)
fmul valC ; ST(0) *= valC
fadd ; ST(0) += ST(1)
fstp valD ; 将 ST(0) 保存到 valD
数组求和
下面的代码计算并显示一个双精度实数数组之和:
ARRAY_SIZE = 20
.data
sngArray REAL8 ARRAY_SIZE DUP(?)
.code
mov esi, 0 ;数组索引
fldz ; 0.0 入栈
mov ecx,ARRAY_SIZE
L1: fld sngArray[esi] ;将内存操作数加载到ST(0)
fadd ; ST(0) 加 ST(1),出栈
add esi,TYPE REAL8 ;移至!I 下一个元素
loop L1
call WriteFloat ;显示 ST(0) 中的和数
平方根之和
FSQRT 指令对 ST(0) 中的数值求平方根,并将结果送回 ST(0)。下面的代码计算了两个数的平方根之和:
.data
valA REAL8 25.0
valB REAL8 36.0
.code
fid valA ; valA 入栈
fsqrt ; ST(0) = sqrt(valA)
fid valB ; valB 入栈
fsqrt ; ST(0) = sqrt(valB)
fadd ; ST (0)+ST(1)
数组点积
下面的代码计算了表达式 (airay[0]*airay[l]) + (array[2]*array[3])。该计算有时也被称为点积 (dot product)。
.data
array REAL4 6.0, 2.0, 4.5, 3.2
下表列出了每条指令执行后,FPU 堆栈的情况。输入数据如下:
| 指令 | FPU堆栈 | 指令 | FPU堆栈 |
|---|---|---|---|
| fld array | ST(0):+6.0000000E+000 | fmul [array+12] | ST(0):+1.4400000E+001 |
| fmul [array+4] | ST(0):+1.2000000E+001 | ST(1):+1.2000000E+001 | |
| fld [array+8] | ST(0):+4.5000000E+000 | fadd | ST(0):+2.6400000E+001 |
| ST(1):+1.2000000E+001 |
12.汇编语言混合模式运算简述
都目前为止,算术运算只涉及实数。应用程序通常执行的是包含了整数与实数的混合模式运算。整数运算指令,如 ADD 和 MUL,不能操作实数,因此只能选择用浮点指令。Intel指令集提供指令将整数转换为实数,并将数值加载到浮点堆栈。
【示例 1】下面的 C++ 代码将一个整数与一个双精度数相加,并把和数保存为双精度数。C++ 在执行加法前,把整数自动转换为实数:
int N = 20;
double X = 3.5;
double Z = N + X;
与之等效的汇编代码如下:
.data
N SDWORD 20
X REAL8 3.5
Z REAL8 ?
.code
fild n ;整数加载到ST(0)
fadd X ;将内存操作数与ST(0)相加
fstp z ;将ST(0)保存到内存操作数
【示例 2】下面的 C++ 程序把 N 转换为双精度数后,计算一个实数表达式,再将结果保存为整数变量:
int N = 20;
double X = 3.5;
int Z = (int)(N + X);
Visual C++ 生成的代码先调用转换函数 (ftol),再把截断的结果保存到 Z。如果在表达式的汇编代码中使用 FIST,那么就可以避免函数调用,不过Z (默认) 会向上舍入为 24:
fild N ;整数加载到ST(0)
fadd X ;将内存操作数与ST(0)相加
fist Z ;将ST(0)保存为整型内存操作数
修改舍入模式
FPU 控制字的 RC 字段指定使用的舍入类型。可以先用 FSTCW 把控制字保存为一个变量,再修改 RC 字段(位 10 和 11),最后用 FLDCW 指令把这个变量加载回控制字:
fstew ctrlWord ;保存控制字
or ctrlWord, 110000000000b ;设置眈=截断
fldcw ctrlWord ;加载控制字
之后采用截断执行计算,生成结果为 Z=23:
fild N ;整数加载到ST(0)
fadd X ;将内存整数与ST(0)相加
fist Z ;将ST(0)保存为整型内存操作数
或者,把舍入模式重新设置为默认选项(舍入到最接近的偶数):
fstcw ctrlWord ;保存控制字
and ctrlWord, 001111111111b ;重置舍入模式为默认
fldcw ctrlWord ;加载控制字
13.汇编语言异常的屏蔽与未屏蔽简述
默认情况下,异常是被屏蔽的,因此,当出现浮点异常时,处理器分配一个默认值为结果,并继续平稳地工作。例如,一个浮点数除以 0 生成结果为无穷,但不会中断程序:
.data
val1 DWORD 1
val2 REAL8 0.0
.code
fild val1 ;整数加载到ST(0)
fdiv val2 ;ST(0) =正无穷
如果 FPU 控制字没有屏蔽异常,那么处理器就会试着执行合适的异常处理程序。清除 FPU 控制字中的相应位就可以实现异常的未屏蔽操作,如下表所示。
| 位 | 说明 | 位 | 说明 |
|---|---|---|---|
| 0 | 无效操作异常屏蔽位 | 5 | 精度异常屏蔽位 |
| 1 | 非规格化操作数异常屏蔽位 | 8〜9 | 精度控制位 |
| 2 | 除零异常屏蔽位 | 10〜11 | 舍入控制位 |
| 3 | 上溢异常屏蔽位 | 12 | 无穷控制位 |
| 4 | 下溢异常屏蔽位 |
假设不想屏蔽除零异常, 则需要如下步骤:
1) 将 FPU 控制字保存到 16 位变量。
2) 清除位 2(除零标志位)。
3) 将变量加载回控制字。
下面的代码实现了浮点异常的未屏蔽操作:
.data
ctrlWord WORD ?
.code
fstcw ctrlWord ;获取控制字
and ctrlWord, 1111111111111011b ;不屏蔽除零异常
fldcw ctrlWord ;结果加载回 FPU
现在,如果执行除零代码,那么就会产生一个未屏蔽异常:
fild val1
fdiv val2 ;除零
fst val2
只要 FST 指令开始执行,MS-Windows 就会显示错误信息。
屏蔽异常
要屏蔽一个异常,就把 FPU 控制字中的相应位置 1。下面的代码屏蔽了除零异常:
.data
ctrlWord WORD ?
.code
fstcw ctrlWord ;获取控制字
or ctrlWord, 100b ;屏蔽除零异常
fldcw ctrlWord ;结果力口载回 FPU
14.汇编语言x86指令编码简述
若要完全理解汇编语言操作码和操作数,就需要花些时间了解汇编指令翻译成机器语言的方法。由于 Intel 指令集使用了丰富多样的指令和寻址模式,因此这个问题相当复杂。
Intel 8086 处理器是第一个使用复杂指令集计算机(Complex Instruction Set Computer, CISC)设计的处理器。这种指令集中包含了各种各样的内存寻址、移位、算术运算、数据传送和逻辑操作。
与 RISC(精简指令集计算机,Reduced Instruction Set Computer)指令相比,Intel 指令在编码和解码方面有些复杂。
指令编码(encode)是指将汇编语言指令及其操作数转换为机器码。指令解码(decode)是指将机器指令转换为汇编语言。对 Intel 指令编码和解码的逐步解释至少将有助于唤起对 MASM 作者们辛苦工作的理解和欣赏。
指令格式
一般的 x86 机器指令格式,如下图所示。包含了一个指令前缀字节、操作码、Mod R/M 字节、伸缩索引字节(SIB)、地址位移和立即数。
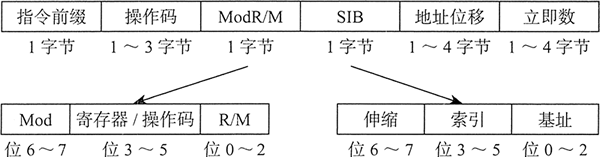
指令按小端顺序存放,因此前缀字节位于指令的起始地址。每条指令都有一个操作码,而其他字段则是可选的。少数指令包含了全部字段,平均来看,绝大多数指令都有 2 个或 3 个字节。
下面是对指令字段的简介:
1) 指令前缀覆盖默认操作数大小。
2) 操作码(操作代码)指定指令的特定变体。比如,按照使用的参数类型,指令 ADD 有 9 种不同的操作码。
3) Mod R/M 字段指定寻址模式和操作数。符号 “R/M” 代表的是寄存器和模式。下表列出了 Mod 字段。
| Mod | 位移 |
|---|---|
| 00 | DISP=0,位移低半部分和高半部分都无定义(除非r/m = 110) |
| 01 | DISP= 位移低半部分符号扩展到 16 位,位移高半部分无定义 |
| 10 | DISP= 位移高半部分和低半部分都有效 |
| 11 | R/M 字段包含的是寄存器编号 |
下表给出了当 Mod=10b 时 16 位应用程序的 R/M 字段。
| R/M | 有效地址 | R/M | 有效地址 |
|---|---|---|---|
| 000 | [BX+SIJ+D16 | 100 | [SI]+D16 |
| 001 | [BX+DI]+D16 | 101 | [DI]+D16 |
| 010 | [BP+SI]+D16 | 110 | [BP]+D16 |
| 011 | [BP+DIJ+D16 | 111 | [BX]+D16 |
4) 伸缩索引字节(scale index byte, SIB)用于计算数组索引偏移量。
5) 地址位移字段保存了操作数的偏移量,在基址-偏移量或基址-变址-偏移量寻址模式中,该字段还可以与基址或变址寄存器相加。
6) 立即数字段保存了常量操作数。
15.汇编语言单字节指令与立即操作数简述
没有操作数或只有一个隐含操作数的指令是最简单的指令。这种指令只需要操作码字段,字段值由处理器的指令集预先确定。下表列出了几个常见的单字节指令。
| 指令 | 操作码 | 指令 | 操作码 |
|---|---|---|---|
| AAA | 37 | LODSB | AC |
| AAS | 3F | XLAT | D7 |
| CBW | 98 | INC DX | 42 |
在这些指令中,INC DX 指令好像是不应该岀现的,它出现的原因是:指令集的设计者决定为某些常用指令提供独特的操作码。其结果是,为了代码量和执行速度要对寄存器增量操作进行优化。
立即数送寄存器
立即操作数(常数)按照小端顺序(起始地址为最低字节)添加到指令。首先关注的是立即数送寄存器指令,暂不考虑内存寻址的复杂性。将一个立即字送寄存器的 MOV 指令的编码格式为:B8+rw dw,其中操作码字节的值为 B8+rw,表示将一个寄存器编号(0〜7)与 B8 相加;dw 为立即字操作数,低字节在低地址。
下表列出了操作码使用的寄存器编号。
| 寄存器 | 编号 | 寄存器 | 编号 |
|---|---|---|---|
| AX/A1 | 0 | SP/AH | 4 |
| CX/CL | 1 | BP/CH | 5 |
| DX/DL | 2 | SI/DH | 6 |
| BX/BL | 3 | DI/BH | 7 |
下面例子中出现的所有数值都为十六进制。
【示例 1】PUSH CX 机器指令为 51。编码步骤如下:
1) 带一个 16 位寄存器操作数的 PUSH 指令编码为 50。
2) CX的寄存器编码为1,因此1+50得到操作码为51。
【示例 2】MOV AX, 1 机器指令为 B8 01 00(十六进制)。编码过程如下:
1) 立即数送 16 位寄存器的操作码为 B8。
2) AX 的寄存器编号为 0,将 0 加上 B8(参见上表所示)。
3) 立即操作数(0001)按小端顺序添加到指令(01, 00 )。
【示例 3】MOV BX, 1234h 机器指令为 BB 34 12。编码过程如下:
1) 立即数送 16 位寄存器的操作码为 B8。
2) BX 的寄存器编号为 3,将 3 加上 B8 得到操作码 BB。
3) 立即操作数字节为 34 12。
从实践的角度出发,建议手动汇编一些 MOV 立即数指令来提高能力,然后通过 MASM 的源列表文件中的生成代码来检查汇编结果。
16.汇编语言寄存器模式指令简述
在使用寄存器操作数的指令中,ModR/M 字节用一个 3 位的标识符来表示寄存器操作数。下表列岀了寄存器的位编码。操作码字段的位 0 用于选择 8 位或 16 位寄存器:1 表示 16 位寄存器,0 表示 8 位寄存器。
| R/M | 寄存器 | R/M | 寄存器 |
|---|---|---|---|
| 000 | AX or AL | 100 | SP or AH |
| 001 | CX or CL | 101 | BP or CH |
| 010 | DX or DL | 110 | SI or DH |
| 011 | BX or BL | 111 | DI or BH |
比如,MOV AX, BX 的机器码为 89 D8。寄存器送其他操作数的 16 位 MOV 指令的 Intel 编码为 89/r,其中 /r 表示操作码后面带一个 Mod R/M 字节。
Mod R/M 字节有三个字段(mod. reg 和 r/m)。例如,若 Mod R/M 的值为 D8,则它包含如下字段:
| mod | reg | r/m |
| 11 | 011 | 000 |
- 位 6〜7 是 mod 字段,指定寻址模式。mod 字段为 11 表示 r/m 字段包含的是一个寄存器编号。
- 位 3〜5 是 eg 字段,指定源操作数。在本例中,BX 就是编号为 011 的寄存器。
- 位 0〜2 是 r/m 字段,指定目的操作数。本例中,AX 是编号为 000 的寄存器。
下表列出了更多使用 8 位和 16 位寄存器操作数的例子。
| 指令 | 操作码 | mod | reg | r/m |
|---|---|---|---|---|
| mov ax, dx | 8B | 11 | 000 | 010 |
| mov al, dl | 8A | 11 | 000 | 010 |
| mov ex, dx | 8B | 11 | 001 | 010 |
| mov cl, dl | 8A | 11 | 001 | 010 |
17.汇编语言处理器操作数大小前缀作用及意义
现在将注意力转回到 x86 处理器(IA-32)的指令编码。有些指令以操作数大小前缀开始,覆盖了其修改指令的默认段属性。问题是,为什么有指令前缀?在编写 8088/8086 指令集时,几乎所有 256 个可能的操作码都用于处理带有 8 位和 16 位操作数的指令。
当 Intel 开发 32 位处理器时,就需要想办法发明新的操作码来处理 32 位操作数,而同时还要保持与之前处理器的兼容性。对于面向 16 位处理器的程序,所有使用 32 位操作数的指令都添加一个前缀字节。
对于面向 32 位处理器的程序,默认为 32 位操作数,因此所有使用 16 位操作数的指令添加一个前缀字节。8 位操作数不需要前缀。
【示例】16 位操作数,现在对 MOV 指令进行汇编,以此为例来看看在 16 位模式下前缀字节是如何起作用的。.286 伪指令指明编译代码的目标处理器,确保不使用 32 位寄存器。下面的每条 MOV 指令都给岀了其指令编码:
.model small
.286
.stack 100h
.code
main PROC
mov ax, dx ; 8B C2
mov al, dl ; 8A C2
现在对 32 位处理器汇编相同的指令,使用 .386 伪指令,默认操作数为 32 位。指令将包括 16 位和 32 位操作数。第一条 MOV 指令(EAX、EDX)使用的是 32 位操作数,因此不需要前缀。第二条 MOV(AX、DX)指令由于使用的是 16 位操作数,因此需要操作数大小前缀(66):
.model small
.386
.stack 100h
.code
main PROC
mov eax,edx ; 8B C2
mov ax,dx ; 66 8B C2
mov al,dl ; 8A C2
18.汇编语言内存模式指令简述
如果 Mod R/M 字节只用于标识寄存器操作数,那么 Intel 指令编码就会相对简单。实际上,Intel 汇编语言有着各种各样的内存寻址模式,这就使得 Mod R/M 字节编码相当复杂。(指令集的复杂性是 RISC 设计支持者常见的批评理由。)
Mod R/M 字节正好可以指定 256 个不同组合的操作数。下表列岀了 Mod 00 时的 Mod R/M 字节(十六进制)。
| 字节 | AL | CL | DL | BL | AH | CH | DH | BH | ||
| 字 | AX | CX | DX | BX | SP | BP | SI | DI | ||
| 寄存器ID | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 | ||
| Mod | R/M | Mod R/M 值 | 有效地址 | |||||||
| 00 | 000 | 00 | 08 | 10 | 18 | 20 | 28 | 30 | 38 | [BX+SI] |
| 001 | 01 | 09 | 11 | 19 | 21 | 29 | 31 | 39 | [BX+DI] | |
| 010 | 02 | 0A | 12 | 1A | 22 | 2A | 32 | 3A | [BP+SI] | |
| 011 | 03 | 0B | 13 | 1B | 23 | 2B | 33 | 3B | [BP+DI] | |
| 100 | 04 | 0C | 14 | 1C | 24 | 2C | 34 | 3C | [SI] | |
| 101 | 05 | 0D | 15 | 1D | 25 | 2D | 35 | 3D | [DI] | |
| 110 | 06 | 0E | 16 | 1E | 26 | 2E | 36 | 3E | 16 位偏移量 | |
| 111 | 07 | 0F | 17 | 1F | 27 | 2F | 37 | 3F | [BX] | |
Mod R/M 字节编码的作用如下:Mod 列中的两位指定寻址模式的集合。比如,Mod 00 有 8 种可能的 R/M 数值(000b〜111b),有效地址列给岀了这些数值标识的操作数类型。
假设想要编码 MOV AX, [Si], Mod 位为 00b, R/M 位为 100b。从《x86指令编码》一节中的 16 位 RM 表中可知 AX 的寄存器编号为 000b,因此完整的 Mod R/M 字节为 00 000 100b 或 04h:
| mod | reg | r/m |
| 00 | 000 | 100 |
十六进制字节 04 在上表(Mod R/M)的 AX 列第 5 行。
MOV [SI], AL 的 Mod R/M 字节还是一样的(04h),因为寄存器 AL 的编号也是 000。现在对指令 MOV [SI], AL 进行编码。8 位寄存器的传送操作码为 88。Mod R/M 字节为 04h,则机器码为 88 04。
MOV 指令示例
下表列出了 8 位和 16 位 MOV 指令所有的指令格式和操作码。
| 操作码 | 指令 | 说明 | 操作码 | 指令 | 说明 |
|---|---|---|---|---|---|
| 88/r | MOV eb, rb | 字节寄存器送 EA 字节操作数 | 8E/2 | MOV SS, rw | 字寄存器送 SS |
| 89/r | MOV ew, rw | 字寄存器送 EA 字操作数 | 8E/3 | MOV DS, mw | 内存字送 DS |
| 8A/r | MOV rb, eb | EA 字节操作数送字节寄存器 | 8E/3 | MOV DS, rw | 字寄存器送 DS |
| 8B/r | MOV rw, ew | EA 字操作数送字寄存器 | A0 dw | MOV AL, xb | 字节变量(偏移量为 dw)送 AL |
| 8C/0 | MOV ew, ES | ES 送 EA 字操作数 | A1 dw | MOV AX, xw | 字变量(偏移量为 dw)送 AX |
| 8C/1 | MOV ew, CS | CS 送 EA 字操作数 | A2 dw | MOV xb, AL | AL 送字节变量(偏移量为 dw) |
| 8C/2 | MOV ew, SS | SS 送 EA 字操作数 | A3 dw | MOV xw, AX | AX 送字寄存器(偏移量为 dw) |
| 8C/3 | MOV ew, DS | DS 送 EA 字操作数 | B0+rb db | MOV rb, db | 字节立即数送字节寄存器 |
| 8E/0 | MOV ES, mw | 内存字送 ES | B8+rw dw | MOV rw, dw | 字立即数送字寄存器 |
| 8E/0 | MOV ES, rw | 字寄存器送 ES | C6 /0 db | MOV eb, db | 字节立即数送 EA 字节操作数 |
| 8E/2 | MOV SS, mw | 内存字送 SS | C7 /0 dw | MOV ew, dw | 字立即数送 EA 字操作数 |
下面两表给出了上表中缩写符号的补充信息。手动汇编 MOV 指令时可以用这些表作为参考。
| /n: | 操作码后面跟一个 Mod R/M 字节,该字节后面可能再跟立即数和偏移量字段。数字 n( 0〜7 )为 Mod R/ M 字节中 reg 字段的值 |
| /r: | 操作码后面跟一个 Mod R/M 字节,该字节后面可能再跟立即数和偏移量字段 |
| db: | 操作码和 Mod R/M 字节后面跟一个字节立即操作数 |
| dw: | 操作码和 Mod R/M 字节后面跟一个字立即操作数 |
| +rb: | 8 位寄存器的编号(0〜7 ),与前面的十六进制字节一起构成 8 位操作码 |
| +rw: | 16 位寄存器的编号(0〜7 ),与前面的十六进制字节一起构成 8 位操作码 |
| db | -128〜+127 之间的有符号数。若操作数为字类型,则该数值进行符号扩展 |
| dw | 指令操作数为字类型的立即数 |
| eb | 字节类型操作数,可以是寄存器也可以是内存操作数 |
| ew | 字类型操作数,可以是寄存器也可以是内存操作数 |
| rb | 用数值(0〜7 )标识的 8 位寄存器 |
| rw | 用数值(0〜7 )标识的 16 位寄存器 |
| xb | 无基址或变址寄存器的简单字节内存变量 |
| xw | 无基址或变址寄存器的简单字内存变量 |
下表列出了更多的 MOV 指令,这些指令能手动汇编,且可以与表中的机器代码比较。假设 myWord 的起始地址偏移量为 0102h。
| 指令 | 机器码 | 寻址模式 |
|---|---|---|
| mov ax, my Word | A1 02 01 | 直接(为 AX 优化) |
| mov my Word,bx | 89 IE 02 01 | 直接 |
| mov[di],bx | 89 ID | 变址 |
| mov[bx+2],ax | 89 47 02 | 基址 – 偏移量 |
| mov[bx+si],ax | 89 00 | 基址 – 变址 |
| mov word prt [bx+di+2], 1234h | C7 41 02 34 12 | 基址 – 变址 – 偏移量 |








Comments NOTHING